احتمال در بلک جک: برای داشتن سود به چه اطلاعاتی نیاز دارید؟

وقتی شخصی از کازینو بیرون می‌رود، سؤالی که ناگزیر در ذهنش ایجاد می‌شود این است که «چرا من باختم؟» بیشتر افرادی که در کازینو بازی می‌کنند، بازنده هستند. دلیلش این است که اکثر بازی‌های کازینو به طور طبیعی انتظار منفی برای بازیکن دارند. این بدان معنی است که برای هر مبلغی که در بازی شرط می‌بندید؛ چه ماشین یا چه بازی روی میز، مقدار کمتری پول در طول زمان به شما بازگردانده می‌شود.

اگر ۱ میلیون بازیکن هر کدام ۱ دلار شرط ببندند و یک بازیکن ۵۰۰ هزار دلار برنده شود، کازینو یک سود ۵۰۰ هزار دلاری می‌کند و هر شرط‌بند به طور متوسط ۵۰ سنت می‌بازد. در ماشین‌های اسلات بازپرداخت تبلیغ شده معمولاً حدود ۹۷-۹۹ درصد خواهد بود. این مقدار بیش از تمام طول عمر دستگاه است که در آن ماشین ممکن است ۱۰۰۰۰ میلیون دلار در طول عمر خود جمع کند. بازی‌های روی میز کمی متفاوت هستند زیرا برخی شامل جزئی موثر به نام مهارت هستند ودرصد سود کازینو از بازیکنی به بازیکن دیگر متفاوت است. اما همین اصل کلی اعمال می‌شود.

این مقاله یک تحلیل عمیق در ریاضیات بازی کازینو می‌باشد. اطلاعات ارائه شده در اینجا برای بازی زندۀ بلک جک و همچنین بازی آنلاین معتبر است. با این حال؛ برنامه‌های نرم‌افزاری بلک جک که کازینوهای آنلاین از آن استفاده می‌کنند شامل همۀ کارت‌ها در هر دور جدید بازی است. این تحلیل در مورد بازی بلک جک اعمال خواهد شد. بلک جک یک بازی با احتمالات پویا و تغییرات درصدها است. اما حتی اگر درصد‌ها به طور مداوم در حال تغییر هستند ، درصد انباشته سود کلی ثابت می‌ماند.

این با در نظر گرفتن مجموع سود در سرتاسر احتمالات ممکن به دست می‌آید. به عنوان مثال ، اگر کل یک دست سود +۵٪ داشته باشد و دست دیگر دارای سود -۶٪ باشد ، سود کل این دو دست + ۱٪ است. هنگامی که خواننده این بازی را درک کند ، ترجمۀ مفاهیم به هر بازی دیگری از کازینو آسان خواهد بود.

آمار بازی

شناخت آمارهای مربوط به بازی کازینو در ارزیابی نتایج ضروری است. این اخبار هم برای بازیکن و هم برای کازینوها معتبر است. دانش ارائه شده در اینجا که از قلمرو احتمالات آماری بدست آمده برای تعیین اینکه نتیجه خوب یا بد می‌شود لازم است.

اکثر بازی‌های شانس بیانگر مفهوم ریاضیاتی هستند که به “قانون آزمایش های مستقل” معروف است. این قانون بیان می‌کند که وقایع گذشته هیچ ارتباطی با وقایع آینده ندارند. این به راحتی در رولت و کرپس نشان داده می‌شود. به عنوان مثال ، هنگامی که یک سکه می‌چرخد ​​، ۵۰٪ احتمال دارد که نتیجه شیر باشد و ۵۰٪ احتمال دارد که نتیجه خط باشد.

اگر سکه ۱۰ بار پشت سر هم شیر باشد ، در پرتاب بعدی هم مجدداً ۵۰٪ احتمال آمدن شیر وجود دارد. در بلک جک ، آنچه در گذشته اتفاق می‌افتد ، مستقیماً روی اتفاقات آینده تأثیر می‌گذارد. بازی بلک جک حافظه دارد ، و قانون آزمایش مستقل در مورد آن معتبر نیست.

چگونه بلک جک متفاوت است؟

در بلک جک هر کارت دارای یک ارزش خاص است که که از سود اولیه‌ای که کازینو نسبت به بازیکن دارد کم می‌شود یا به آن اضافه می‌شود. سود اولیه برگرفته از قوانین بازی است. وقتی تعداد کافی از کارت‌های مناسب پخش می‌شود ، سود به نفع بازیکنان تغییر می‌کند. در بلک جک هنگامی که یک کارت تک خال یا ۱۰ پخش می‌شود سود کازینو نسبت به بازیکن افزایش می‌یابد. هنگامی که کارت‌های با ارزش کمتر در بازی قرار می‌گیرند (۲-۷) سود کازینو کاهش می‌یابد ، و هنگامی که به تعداد کافی از آن کارت‌ها در بازی قرار گیرند ، بازیکن سود بیشتری نسبت به کازینو دارد.

درصد سودی که کازینو نسبت به بازیکن دارد (در بلک جک) یا برعکس ،سود بازیکن نسبت به کازینو  ثابت نیست. راه ‌حل‌های زیادی وجود دارد که می‌توان آن‌ها را معرفی کرد تا درصد‌های در حال تغییر را پیگیری کرد. ساده‌ترین موردی که به میزان کمتری در معرض خطای بازیکن قرار دارد سیستم شمارش Hi / Lo است. در این سیستم ارقام ۱ ، -۱ یا ۰  به عنوان ارزش به هر کارت تعلق می‌گیرد. به کلیۀ کارتهای ۲-۶ رقم ۱ اختصاص داده می‌شود و به کلیۀ کارت‌های با ارزش ۷ ، ۸ و ۹ رقم ۰ داده می‌شود. کلیۀ ده‌ها ، کارت‌های صورت و تک خال‌ها دارای ارزش -۱ هستند. با پخش شدن کارت‌ها ، بازیکن ارزش کارت‌ها را جمع می‌کند، مجموع بدست آمده این کارت‌ها پس از یک دور بازی ، شمارش جاری نامیده می‌شود.

در یک شمارش جاری مثبت ، ارزش به صورت تعداد کارت‌های با ارزش موجود نسبت به تعداد کارت‌های کم ارزش موجود در یک دسته کارت سنجیده می‌شود (یا کارت‌های کم ارزش نسبت به کارت‌های با ارزش). برای دستیابی به این هدف ، بازیکن تخمین می‌زند که چند دسته کارت باقی مانده است ، و سپس شمارش جاری را بر تعداد دسته کارت موجود تقسیم می‌شود ، و این ارزش به دست آمده با عنوان شمارش واقعی نامیده می‌شود. به عنوان مثال ، اگر یک بازیکن مشاهده کرد که از شش دسته کارت موجود در دستگاه کارت پخش کن سه دسته از آن بازی شده است، و شمارش در حال اجرا ۱۵ است، که به این معنی است که در طول این سه دسته کارتی که بازی شده است ۱۵ عدد کارت کم ارزش نسبت به کارت‌های با ارزش بیشتر بازی شده است، برای بدست آوردن رقم شمارش واقعی باید رقم شمارش جاری یعنی ۱۵ را تقسیم بر تعداد دسته کارت باقی مانده یعنی ۳ بکند که عدد ۵ بدست می‌آید.

بازیکن رقمی را به عنوان میزان انحراف که معمولا ۱ است تفریق می‌کند.که این رقم برتری کازینو را در صفر بازی در نظر می‌گیرد.( این رقم به عوامل زیادی من جمله قوانین بازی و تعداد دسته کارت موجود در بازی بستگی دارد ) و آن تعداد، تعداد واحدهایی است که بازیکن در دست بعدی شرط‌بندی خواهد کرد. برای هر افزایش واحد کل (مثبت یا منفی) که در شمارش واقعی مشاهده می‌شود ، سود بازیکن به ترتیب تقریباً ۰٫۵٪ ، مثبت یا منفی افزایش می‌یابد.

وقتی کارت‌های با ارزش تعداد بیشتری دارند، رقم شمارش واقعی بالا خواهد بود و بازیکن نسبت به کازینو برتری دارد. این به سه دلیل اتفاق می‌افتد. اول اینکه دست با ارزش بلک جک بیشتر اتفاق می‌افتد و، به دلیل اینکه پرداخت روی یک بلک جک نامتوازن است (به بازیکن در صورت آوردن بلک جک ۳:۲ پرداخت می‌شود در صورتی که اگر دیلر بلک جک بیاورد فقط شرط اولیۀ خود را خواهد باخت )، این به نفع بازیکن است.دوم اینکه برخی شرایط برای بازیکن با ارزش‌تر می‌شوند، مثل تقسیم کردن و دوبل کردن.

معمولاً یک بازیکن دوست دارد وقتی دوبل یا تقسیم می‌کند ، کارت بالایی بیرون آورده شود ، یا در حالت دیگر بازیکن در هنگام ضعیف بودن دیلر از این گزینه ها استفاده می‌کند و یک کارت بالا باعث شکست دیلر می‌شود (کارتی که باعث می شود دیلر بیشتر از ۲۱ شود). این بازی‌ها وقتی که کارت‌های باقی مانده در دستگاه با ارزش هستند بازپرداخت بالاتری برای بازیکن دارند.

در آخر، بازیکن ممکن است بسته به ترکیب کارت‌های باقیمانده ، استراتژی خود را تغییر دهد. با فزونی کارت‌های بالا ، بازیکن می‌تواند روی دست های قوی‌تر بایستد (مجموع ۱۲-۱۶) ، با مجموع قوی بیشتر از اوقات دیگر دوبل کند (کارت های برابر با ۹ ، ۱۰ یا ۱۱) و یا ، هنگامی که دیلر ضعیف و مستعد است که بالای ۲۱ رود ، بازیکن ممکن است بایستد. در مقابل ، قوانین دیلر را از تغییر استراتژی منع می‌کند. در نهایت ترکیب این عوامل شرایطی ایجاد می‌کند که سود صفر کازینوها بر طرف شوند و یک بازیکن ماهر نسبت به کازینو برتری داشته باشد.

محاسبه پیروزی

برای تعیین مبلغی که شخص انتظار دارد در یک زمان معین (یا کازینو یا بازیکن) برنده شود ، سه دسته اطلاعات کلیدی نیاز است.

۱٫ مبلغ شرط

۲٫ تعداد دست‌ها یا چرخش‌ها

۳٫ درصد برتری

 در فرم معادله، آنچه که توضیح داده شد به این صورت است:

مبلغی که انتظار می‌رود پیروز شوید = مبلغی که شرط‌بندی می‌کنید * احتمال پیروزی ٪ * # تعداد دستی که بازی خواهید کرد

معادله ۱

اگر معادله‌ای که عنوان شد را برای پرتاب یک سکه در نظر بگیریم، میدانیم که سکه دو طرف دارد، بنابراین ۵۰ درصد احتمال دارد که نتتیجۀ پرتاب شیر باشد و ۵۰ درصد خط. وقتی در هر پرتاب سکه ۱ دلار شرط بندی کنیم جواب معادله برای مبلغی که انتظار داریم پیروز شویم در ۱۰۰ پرتاب به این صورت است:

۵۰ دلار = ۱ $ (شرط بندی) * ۰٫۵٪ (٪ مزیت) * ۱۰۰ (# دست بازی)

معادله ۲

در این مثال ما ۱۰۰ دلار شرط‌بندی کرده‌ایم و ۵۰ دلار از ۵۰ شرط  بندی کسب کردیم. ما همچنین قادر بودیم شرط اصلی ۱ دلار را روی ۵۰ تا از ۱۰۰ شرط مذکور حفظ کنیم. همچنین در هر ۵۰ شرط ۱ دلار از دست دادیم. این منجر به یک بازی با جمع صفر می‌شود. بدون برنده و بدون بازنده.

آیا من جایی هستم که باید باشم؟

هنگامی که یک سکه ۱۰۰ بار پرتاب می‌شود ​​نتیجه پرتاب به ندرت پنجاه بار شیر و پنجاه بار خط خواهد بود. بنابراین باید مفهوم واریانس را معرفی کنیم. واریانس اندازه گیری پراکندگی آماری است. به عبارتی دیگر، این واحد با میزان فاصله‌ای که نتیجه مورد انتظار با نتیجۀ یک امتحان یا آزمایش ممکن است داشته باشد سر و کار دارد.

مثلاً در مثال پرتاب سکه ، واریانس به ما کمک می‌کند که جواب این سوال را بدهیم. این سؤال که در پرتاب ۱۰۰ سکه ۴۵ بار شیر داشته باشیم ، تعجب آور خواهد بود یا فقط ۵ بار. پاسخ ها خیر و بله است. دریافت فقط ۵ شیر در پرتاب ۱۰۰ بار پرتاب سکه نشان می‌دهد که شما در حال پرتاب یک سکۀ سنگین هستید. درک این مفهوم برای ارزیابی نتایج بازی‌های کازینو بسیار مهم است ، زیرا برای تعیین اینکه آیا نتایج (خوب یا بد) تابعی از شانس یا مهارت است ، تجزیه و تحلیل آماری مناسب لازم است. در اصل این معیار تعیین می‌کند که آیا بازیکن یا کازینو را فریب داده‌اند یا خیر.

واریانس معمولاً از نظر انحراف معیار مورد بحث قرار می‌گیرد و این مورد در این بحث پیش می‌رود. انحراف استاندارد برابر با ریشۀ مربع واریانس است. انحراف استاندارد برای یک سری آزمایشات با حرف یونانی σ (sigma) نشان داده می‌شود و برابر با انحراف استاندارد هر رویداد ضرب در ریشه مربع تعداد حوادث است. بیان معادلۀ ریاضی آن به این صورت است:

σ  (کل) = σ (رویداد) *  (تعداد رویدادها) √

معادله ۳

شکل زیر نشان می دهد که چگونه نتایج احتمالی در یک ، دو و سه انحراف استاندارد از نتایج مورد انتظار قرار می‌گیرند. در نمای گرافیکی مقدار پیش بینی شده(expected value) با حرف یونانی μ نشان داده شده و انحراف استاندارد(standard deviation) با حرف یونانی σ نشان داده شده است.

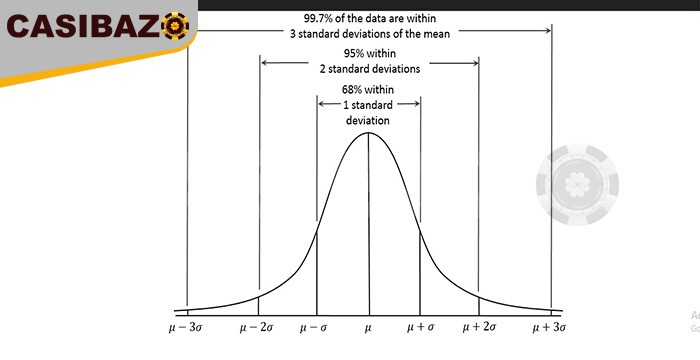
مطابق منحنی توزیع گاوسی ، تقریباً بیش از ۶۸٪ شانس وجود دارد که نتیجه در یک انحراف معیار قرار گیرد ، مثبت یا منفی مقدار مورد انتظار. تقریباً بیش از ۹۵٪ شانس وجود دارد که نتایج در دو انحراف معیار قرار بگیرند ، مثبت یا منفی مقدار مورد انتظار. تقریباً ۹۹٫۹٪ شانس وجود دارد که نتایج در هر زمان معین در سه انحراف معیار قرار بگیرند.

در مثال پرتاب سکه نتیجه می‌گیریم که انحراف استاندارد برای ۱۰۰ بار پرتاب ۱۰ برابر (ریشه مربع ۱۰۰) انحراف استاندارد برای یک بار پرتاب (که ۰٫۵ است) است ، که انحراف استاندارد ۵ برای ۱۰۰ بار پرتاب سکه را نتیجه می‌دهد. در سناریوی ۱۰۰ بار پرتاب سکه انتظار داریم ۵۰ بار شیر و ۵۰ بار خط داشته باشیم. با در نظر گرفتن مفهوم انحراف استاندارد مثبت یا منفی ۵ ، ۶۸٪ احتمال دارد که برای ۱۰۰ بار پرتاب سکه تعدا شیرها بین ۴۵ تا ۵۵ بار باشد.

احتمال ۹۵٪ وجود دارد که تعداد شیرها بین ۴۰ تا ۶۰ باشد (۲ * σ ) و احتمال ۹۹٫۹٪ وجود دارد که تعداد شیرها بین ۳۵ تا ۶۵ سقوط کند (۳ * σ).

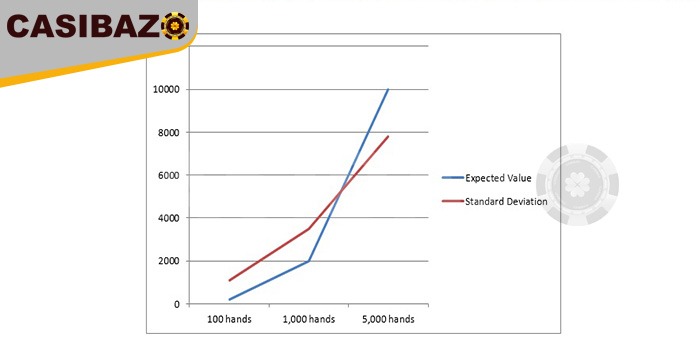
با استفاده از معادلات مقدار پیش‌بینی شده و انحراف معیار در واحد شرط بندی ۱۰۰ دلار برای یک بازی کازینو با یک امتیاز ۱٪ کازینو نسبت به بازیکن ، نتایج زیر بدست می‌آید.

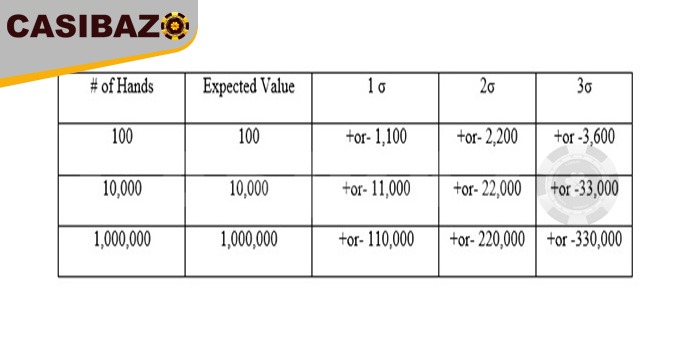از لحاظ گرافیکی به شرح زیر است.

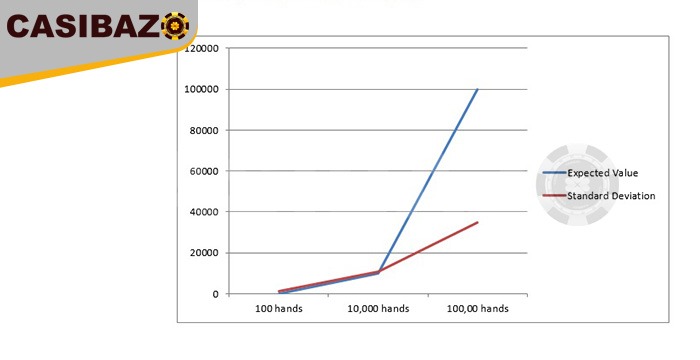
با افزایش تعداد رویدادها ، انحراف استاندارد نسبت به مقدار پیش‌بینی شده کوچکتر و کوچکتر می شود. در برخی از نقاط در امتداد منحنی ، مقدار پیش‌بینی شده و انحرافات استاندارد همدیگر را قطع می‌کنند. در این مرحله ۸۴٪ شانس وجود دارد که انحراف استاندارد کمتر از مقدار پیش‌بینی شده باشد. این بدان معناست که ۸۴٪ شانس وجود دارد که سود حاصل از آن نقطه به دست بیاید و بودجه شما هرگز از بین نرود. این نقطه تقاطع برای مزیت ۱٪ در نمودار زیر نشان داده شده است.

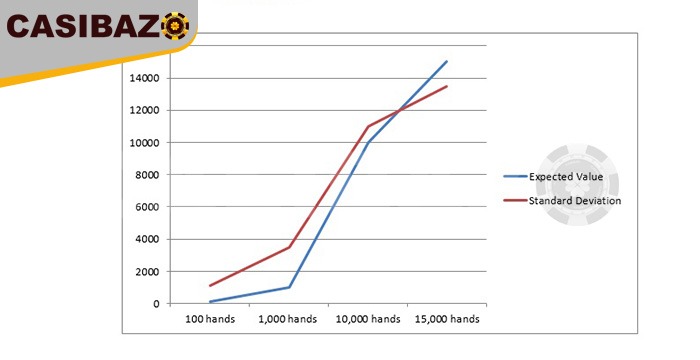
برای ساده سازی انحراف استاندارد معیار خالص است

نقطۀ تقاطع بین مقدار پیش‌بینی شده و انحراف استاندارد دقیقاً زیر ۱۲۰۰۰ دست است. در ۱۲،۰۰۰ دست ۸۴٪ شانس وجود دارد که مقدار پیش‌بینی شده از انحراف معیار استاندارد فراتر رود ، که نشان می دهد بازیکن موجودی بانکش را در۸۴٪ از وقت خود به صفر نمی‌رساند. هنگامی که مزیت کلی به نقطه “هم ارزی”  افزوده می‌شود ، یا تعداد دست‌هایی که مقدار پیش‌بینی شده با انحراف معیار برابر است ، به دست‌های کمتری می رسند. محاسبه همان نمودار با ۲٪ مزیت نموداری خواهد بود که نشانگر نقطه‌ی هم ارزی است که به شکل قابل ملاحظه‌ای پایین تر است.

برای ساده سازی انحراف استاندارد معیار خالص است

در تجزیه و تحلیل نهایی ، کازینوها می توانند خیلی سریع به نقطه “هم ارزی” برسند. این منطقی است زیرا کازینوها روزانه ۲۴ ساعت و ۷ روز در هفته بازی را انجام می‌دهند. و از آنجا که تقریبا همه بازیکنان با ضرر بازی می‌کنند ، کازینوها با واریانس کمتر و کمتر نسبت به مقدار پیش بینی شدۀ خود ، درآمد بیشتری کسب می‌کنند. در مقاله‌های بعدی در مورد جنبه‌های مختلف حمله به بازی‌های کازینو برای کسب سود بحث خواهم کرد.